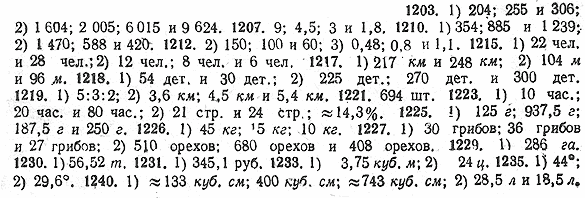ГЛАВА  VIII.

ПРОПОРЦИИ.

ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ   ВЕЛИЧИН.

§ 47.   Пропорциональное  деление.

1200.   Число 135 разделить на части пропорционально числам: 1) 2 и 3; 2) 7 и 8;  3)   1;  3 и   5;   4)   ²/₃ ; 3 и 5¹/₃

1201.   1)   Число 2400  разделить на части пропорционально числам: 2; 3; 8   и  11¹/₅

2) Число 78117 разделить  на части  пропорционально числам ¹/₁₂;  ¹/₄;  ²/₃;  1 и 1¹/₄

1202.  Число   196   разделить на   части   пропорционально   числам: 1) 3; 7 и 11; 2) ¹/₃;   1¹/₃ и 3.

ответы

1203.   1)   Число   765   разделить   на   части   пропорционально числам ¹/₅;¹/₄ и 0,6.

2) Число 19 248 разделить на части пропорционально числам 0,8; 1; 3 и 4,8.

1204. Число 5 005 разделить на части обратно пропорционально числам: 1) 2 и 3; 2) 4 и 7; 3) 3 и 10; 4)¹/₃ и ¹/₄;5) 2 и ¹/₂.

1205. Число 343 разделить на части обратно пропорционально числам: 1) 1; 4 и 9; 2)1;¹/₃ и ¹/₆

1206. Число 136 разделить на части: 1) прямо пропорционально числам 1; 2 и 5; 2) обратно пропорционально числам 1;2 и 5.

1207. Число 18,3 разделить на части обратно пропорционально числам 1; 2; 3 и 5.

1208. Число 434 разделить на части обратно пропорционально числам: 1) 15 и 16; 2) 2; 3 и 5.

1209. Число 3 285 разделить на части обратно пропорционально числам: l)¹/₂ ; 0,3 и 1¹/₃; 2) 1;  ⁵/₇ и 1¹/₄

1210.  Число 2 478 разделить на части:   1)   прямо  пропорционально  числам   2;  5   и    7;   2)   обратно   пропорционально   числам 2; 5 и 7.

1211.  Число   86,7   разделить, на  части   обратно   пропорционально числам 1; 3; 5 и 6.

1212.  1) Разделить число   144   на   три   части: х, у и z, так, чтобы х : у =3 : 4; y : z = 4:5.

2)  Разделить число 310 на три части:  х, у и z, так, чтобы х : у =3 : 2; y : z  = 5 : 3.

3)  Разделить число 2,38 на три части:  х, у и z,   так,   чтобы х : у = 3 : 5; y : z =8 :11.

1213.   1) При   пайке   изделий   из   жести   применяется   сплав «третник»,   содержащий одну  часть свинца  и  две части олова Сколько свинца и олова содержится в 120 г сплава?

2) Латунь представляет собой сплав меди и олова. Сколько меди и сколько олова в 540 г латуни, если количество олова со ставляет 50% количества меди?

1214.   1) На два класса было получено 504 тетради и 126 карандашей. Как распределить тетради и карандаши между классами, если в одном классе 35 человек, а в другом 28 человек?

2) Две школы закупили для коллективного просмотра билеты в кинотеатр и заплатили 90 руб. Сколько следует уплатить каждой школе, если в одной из них 288 учащихся, а во второй 312?

1215.   1) В колхозе с двух участков в 8,25 га и  10,5 га собрали урожай. Нужно было собрать с этих участков оставшиеся колосья. 50 пионеров взялись выполнить эту работу и разбились на две группы   пропорционально   площади  участков.   Сколько пионеров было в каждой группе?

2) Для озеленения школьного участка нужно разбить три клумбы площадью 84 кв. м, 56 кв. м и 42 кв. м. Из 26 человек, изъявивших желание принять участие в разбивке клумб, были созданы три бригады, причём число человек в каждой бригаде было пропорционально площади клумб. Сколько человек было в каждой бригаде?

ответы

1216.   1) Для учащихся шестых классов были получены билеты и распределены  пропорционально  числу  учеников в этих классах. Сколько было  прислано  билетов  и   сколько  получил каждый класс, если в VI А было 36 человек, в VI Б 32 и в VI В 28, причём VI А получил на 12 билетов меньше, чем VI Б и VI В вместе?

2) Воспитанники детского дома выехали на дачу, где поселились в четырёх комнатах, площади которых были равны 56 кв. м, 49 кв. м, 42 кв. м и 35 кв. м, причём число человек в комнатах было пропорционально их площади. Сколько человек было в каждой комнате, если в большей комнате было на 6 человек больше, чем в меньшей?

1217.  1) Некоторое расстояние пассажирский поезд проходит за 10,5 часа, а товарный за 12 час. Где произойдёт встреча поездов, если они одновременно выйдут из двух городов, расстояние между которыми 465 км?

2) Первый спортсмен пробегает 100 м за 12 сек., а второй за 13 сек. Сколько метров пробежит каждый спортсмен до встречи, если они начнут бег одновременно и навстречу друг другу, разойдясь на 200 м?

1218.  1) Мастер изготовляет одну деталь за 5 мин., а ученик изготовляет   такую  же деталь за 9 мин.    Работая вместе, они изготовили  84   детали.    Сколько    деталей   изготовил    мастер и сколько ученик?

2) Один рабочий выполняет норму за 6 час, другой за 5 час. и третий за 4,5 часа. Работаявместе, они изготовили 795 деталей. Сколько деталей изготовил каждый рабочий?

1219.   1) Раскладывая одинаковые по величине бруски, мальчик заметил, что на определённом расстоянии можно уложить в ряд: по длине 6 брусков, по ширине 10 брусков,  по толщине (высоте)15 брусков. Найти отношение длины, ширины  и  толщины брусков.

2) (Задача-шутка.) Колхозник поехал на луга за сеном и взял с собой трёх сыновей: 15 лет, 12 лет и 10 лет. Обратный путь в 13,5 км мальчики по очереди ехали на возу, причём расстояние распределили обратно пропорционально возрасту. Сколько километров проехал каждый из них на возу?

1220.   1) Как распределить между жильцами плату   за   электроэнергию в сумме 1 руб. 44 коп., если в первой комнате горит лампа в 60 ватт, во второй   в   100  ватт, в   третьей  две   лампы по 40 ватт и в четвёртой две лампы по 60 ватт?

2) Три семьи наняли сообща машину для переезда на дачу и уплатили 11 рублей. Дачи были расположены вдоль одного шоссе на расстоянии 24 км, 28 км и 36 км от города. Сколько следует уплатить за машину каждой семье, если они условились платить пропорционально расстоянию?

1221.  Мать послала трёх  сыновей:   Володю   12   лет, Серёжу 10 лет и Андрюшу 8 лет — в лес   за   шишками   для   самовара. По дороге мальчики решили набрать 600 сосновых шишек и распределили это задание между собой пропорционально   возрасту. Возвращаясь домой, мальчики подсчитали,   что   Володя   перевыполнил задание на 20%, Серёжа   на 15% и Андрюша   на   10%. Сколько шишек принесли мальчики из лесу?

1222.  При посадке фруктовых садов   в центральных   районах РСФСР  рекомендуется, чтобы число яблонь,  груш  и   косточковых деревьев относилось, как 10:3:7. Сколько яблонь, груш и косточковых деревьев следует посадить на прямоугольном участке размером 96 м х 60 м,  если каждое дерево  занимает 48 кв. м?

ответы

1223.  1) Группа геологов находилась   в   пути   четверо   суток и 14 час. Третью часть пути геологи проехали на поезде, третью часть на пароходе и третью часть на лошадях. Сколько времени провели геологи в поезде, на пароходе и сколько ехали на лошадях, если средняя скорость передвижения на лошадях   в   8 раз меньше скорости передвижения на поезде и в   4   раза   меньше, чем на пароходе?

2) Первая машинистка выполняет определённую работу за 5 час. 20 мин., а вторая за 4 часа 40 мин. Однажды, работая вместе, они напечатали 45 страниц. Сколько страниц напечатала каждая машинистка и на сколько процентов вторая напечатала больше, чем первая?

1224.   1) На окраску стен в помещении нужно 36 кг краски. Во время ремонта решили   окрасить   стены   в  два   цвета: верх светлой краской, а низ тёмной. Сколько понадобится той и другой краски, если высота стен 3 м, а высота стены, окрашенной в тёмный цвет, 1,8 м? 1,75 м? 1,6  м?

2) В состав менделеевской замазки, не боящейся разведённых кислот, входит 1% льняного масла, канифоль, жедтый воск и безводная окись железа (мумия) в отношении 20:5:8. Сколько составных частей нужно для получения 2,5 кг замазки?

1225. 1) Клей для стекла содержит ¹/₁₂  льняного масла, канифоль, желтый воск и гуттаперчу в отношении 15:3:4 Сколько составных частей нужно для получения 1,5 кг клея?

2) Клейстер, пристающий к стеклу и металлу, приготовляют из крахмала, мела, 20-процентного раствора едкого натра и воды, беря составные части в отношении 1:8:5:25. Сколько граммов каждой из составных частей, а также едкого натра нужно для получения 900 г клейстера? (Вычислить с точностью до 1г)

1226.   1) Колхоз продал некоторое количество мяса трёх сортов;   первого сорта   по   1,2  руб.,   второго  сорта  по  0,9  руб.  и третьего сорта по 0,6 руб. за 1 кг. Первого сорта было продано на 30 кг больше, чем второго; число килограммов второго сорта относилось к числу килограммов третьего сорта, как 3 : 2. Сколько килограммов каждого сорта было   продано, если   в   среднем цена одного килограмма оказалась равной 1,05 руб.?

2) Колхоз разбил фруктовый сад на прямоугольном участке размерами 240 м  х 144 м. Сколько яблонь нужно посадить в саду, если расстояние между рядами деревьев должно быть 8 м, а между деревьями в каждом ряду 6 м? Сколько саженцев зимних, осенних и летних сортов яблонь нужно приобрести, чтобы количества зимних и осенних сортов относились, как 5 : 3, а летних сортов было бы на 72 дерева меньше, чем осенних?

1227.  1) Три девочки нашли в лесу 93 белых   гриба.   Когда первая девочка разложила свои грибы в кучки по пяти  грибов в каждой, а вторая — в кучки  по шести   грибов   в   каждой, то кучек получилось у них поровну.  Когда   же   вторая разложила свои грибы по четыре, а третья — по три, то кучек у них получилось тоже поровну. Сколько  грибов  нашла   каждая девочка?

2) Три мальчика пошли в лес за орехами. При подсчете собранных орехов оказалось, что число орехов у первого мальчика относилось к числу орехов второго, как 3:4, а отношение числа  орехов второго мальчика к числу орехов третьего равно 5:3. Сколько орехов собрал каждый, если у первого мальчика было на 102 ореха больше, чем у третьего?

1228. 1) Срочный заказ на сумму 154 280 руб. поручили выполнять одновременно трём заводам. Как распределили заказ заводы между собой, если производительность первого и второго заводов относится, как 5:3, а производительность третьего завода на 25% меньше, чем производительность первого и второго заводов вместе?

2) С трёх участком собрали 99,75 т картофеля. Количество картофеля, собранного с первого и второго участков, относилось, как 7: 10, а с третьего участка собрали на 15% больше, чем со второго участка. Сколько картофеля собрали с каждого участка?

1229.   1) 30% площади лесного участка занимают лиственные породы деревьев. Остальная площадь занята сосновым и еловым лесом, причём площади этих лесов относятся, как 1,5 : ²/₃.   Определить площадь лесного участка, если сосновый лес занимает на 77 га больше, чем еловый.

2) За первый день тракторная бригада вспахала 32,5% колхозного поля, а площади, вспаханные во второй и третий день, относились, как 0,25:0,2. Определить площадь поля, если во второй день было вспахано на 32,75 га больше, чем в третий.

ответы

1230.   1)  Картофель засыпали в три овощехранилища в отношении 1,3:2¹/₂:1 ¹/₅, причём во втором овощехранилище оказалось на 43,2 т больше, чем в первом. За месяц израсходовали: из первого 40%, из второго 30% и из третьего 25% имевшегося там картофеля. Сколько всего картофеля израсходовали за месяц?

2) Площади трёх лесных участков относятся, как 2,25:1,5:1⁵/₆ , причём площадь третьего на 136 га меньше площади первого. На первом, втором и третьем участках вырубили соответственно 15%, 10% и 5% площади. На какой площади был вырублен лес?

1231.   1) Пионеры собрали 27,2 т металлического лома. 12,5% всего собранного лома было оценено по 4 руб. за 1 т. Остальной лом был рассортирован на две части в отношении 3 : 4 и оценён по 12,5 и 15 руб. за 1 т. Сколько стоил весь лом?

2) На строительную площадку завезли 127,5 т материалов. Алебастр составил 4% всех привезённых материалов, а остальное составляли цемент и известь в отношении 4:5. Сколько алебастра, цемента и извести завезли на строительную площадку?

___________

ответы

1232.   1) Было куплено 240 кг картофеля по 0,04 руб. за 1 кг и 80 кг по 0,06 руб. за 1 кг. Найти среднюю цену картофеля.

2) Смешано 20 т железной руды, содержащей 72% железа, и 28 т железной руды, содержащей 40% железа. Определить процентное содержание железа в получившейся смеси.

1233.   1) Леспромхоз  заготовил  25 куб.  м  берёзовых дроз, 75 куб. м сосновых дров  и 85 куб. м осиновых дров. Сколько кубических метров дров смешанной породы можно погрузить на полуторатонную машину, если  1  куб. м берёзовых дров весит 495 кг, сосновых 425 кг, осиновых 350 кг?

2) В колхозе одна бригада получила средний урожай пшеницы 22,5 ц с 1 га на площади 16,8 га, а вторая 25 ц с 1 га на площади в 25,2 га. Найти средний урожай с 1 га в колхозе.

1234.  1) Для  компота купили   400   г сушёных яблок, 200 г урюка и 150 г изюму.  Найти цену 1 кг смеси,     если 1 кг сушеных яблок стоит 0,9 руб., 1 кг урюка 0,84 руб. и 1 кг изюму 1,6 руб.

2) Из 3.5 кг яблок ценой по 0,6 руб., 6,5 кг яблок ценой по 0,5 руб.  и 9 кг сахарного песку по 0,94 руб.   сварили   варенье. Найти стоимость 1 кг варенья, если вес его составляет 80% веса песка и очищенных яблок. При очистке яблок потери составляют  10%

1235.  1) Из закипевшего чайника вылили   ²/₃  воды, а  оставшийся кипяток долили   водой,   температура   которой была   16°. Определить температуру воды в чайнике.

2) Из закипевшего чайника вместимостью 4,5 л воды вылили 3,6 л и долили чайник водой, температура которой была равна 12°. Определить температуру воды в чайнике.

1236.   1) В ванну, где было 78 л  воды  с   температурой 15°, вылили   два   ведра   кипятку   (температура    100°).   Определить температуру воды в ванне, если ёмкость ведра 12 л.

2) В кадку налито 70 л воды, температура которой равна 4°. Сколько литров воды с температурой 80° нужно налить в кадку, чтобы температура воды поднялась до 24°?

1237.   1) Сплавили два   слитка   серебра:   600-й   пробы   весом 180 г и 875-й пробы весом 216 г. Определить пробу сплава.

2) Сплавлены два слитка золота: 900-й пробы весом 320 г и 540-й пробы весом 160 г. Определить пробу сплава.

1238.   1) Сколько серебра 500-й пробы и 800-й   пробы  нужно сплавить, чтобы получить 225 г серебра 720-й пробы?

2) Сколько золота 600-й пробы и 900-й пробы нужно сплавить, чтобы получить 350 г 720-й пробы?

1239.   1) Сплавили 50 г золота 560-й пробы со слитком эолота неизвестной пробы и получили 300 г золота 760-й пробы.   Определить пробу второго слитка.

2) Сплавили 120 г серебра 640-й пробы со слитком серебра неизвестной пробы и получили 320 г серебра 700-й пробы. Определить пробу второго слитка.

1240.   1) Для консервирования   применяют спирт   крепостью 90°, 80° и 70°. Сколько воды нужно прибавить к 2 л спирта крепостью 96°, чтобы   получить   спирт   указанной   крепости?

2) Для консервирования применяют 2- и 3-процентный раствор формалина. Сколько воды нужно прибавить к 1,5 л 40-процентного раствора формалина, чтобы получить раствор, нужный для консервирования?

ОТВЕТЫ