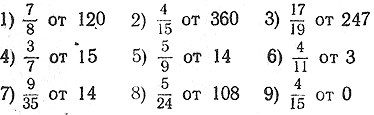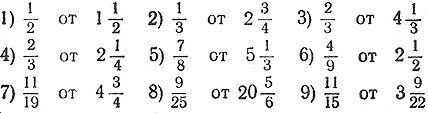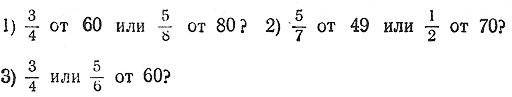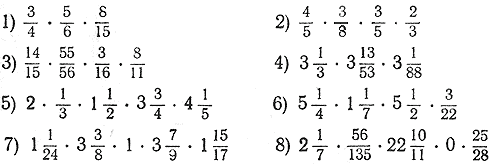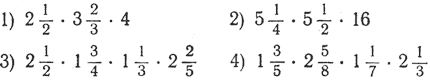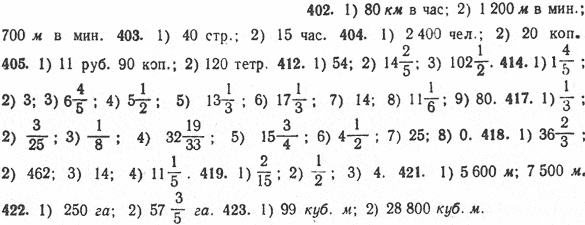|
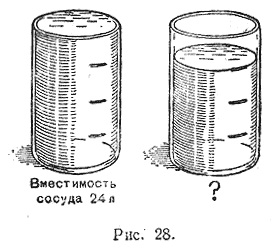
ГЛАВА II. ОБЫКНОВЕННЫЕ ДРОБИ. § 17. Умножение дробей. № 393—396 устно. 393. 1) 1 кг конфет стоит 2 руб. Сколько стоит 1/2 кг этих конфет? 1/4 кг? 3/4 кг? 5/8 кг? 11/2 кг? 21/4 кг? 2) По данным рисунка 28 составьте задачу и решите её.
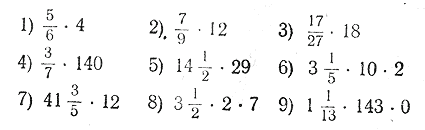
394. 1) Рабочий имел 84 руб.; 3/14 этих денег он израсходовал на покупку часов. Сколько стоят часы? 2) Длина реки Невы равна 37/64 длины канала имени Москвы, протяжение которого равно 128 км. Найти длину Невы. 395. Найти:
396. Найти:
397. Найти:
398. Найти:
399. Найти:
400. Что больше:
401. Найти:
402. 1) Наибольшая скорость автомобиля «Победа» 120 км в час, а наибольшая скорость автомобиля «Москвич» 2/3скорости «Победы». Найти наибольшую скорость автомобиля «Москвич». 2) Скорость полёта стрижа 1600 м в минуту, скворца 3/4 и ястреба 7/16 скорости полёта стрижа. Найти скорость полёта скворца и ястреба в минуту. 403. 1) Книга содержит 140 страниц текста. Ученик прочитал 5/7 всей книги. Сколько страниц ему осталось читать? (Решить двумя способами.) 2) На вопрос: «Который час?», ответили, что оставшаяся часть суток равна 3/8 целых суток. Который был час? 404. 1) В первый день зимних каникул на ёлке в Кремле было 5600 учащихся. Число учащихся старших классов составляло 3/7 общего числа. Сколько было на ёлке учащихся старших классов? 2) У мальчика было 72 коп.; на 5/6 всех денег он купил 3 книги по одинаковой цене. Сколько стоит каждая книга? 405. 1) Имея 25 руб. 50 коп., покупатель израсходовал в одном магазине 1/5 своих денег, а в другом 1/3 . Сколько денег у него осталось? 2) В киоск доставили 960 тетрадей; 5/8 этого количества было в одну линейку, 1/4 в клетку, а остальные в две линейки. Сколько доставили тетрадей в две линейки? 406. Составить задачи, для решения которых требуется умножить: 1) 40 км на 3/4 2) 60 кг на 2/5 3) 2 т на 1/3 407. Найти произведения:
408. Увеличить 31/2 в 6 раз, выполнив умножение двумя способами: 1) обратив 31/2 в неправильную дробь; 2) использовав распределительный закон умножения. 409. Выполнить умножение двумя способами:
410. Найти произведения:
412. Выполнить умножение двумя способами (см. № 408) и выяснить, какой способ проще:
Найти произведения:
415. Не выполняя умножения, определить, что больше:
416. В каких случаях при умножении числа на дробь в произведении получится число: 1) меньше множимого, 2) равное множимому и 3) больше множимого? Составить по 2 примера, поясняющих каждый случай. 417. Найти произведения:
418. Выполнить умножение, взяв сомножители в том порядке, как они записаны; затем выполнить умножение, переменив порядок сомножителей. Сравнить полученные результаты:
419. Выполнить умножение, взяв сомножители в том порядке, как они записаны; затем, соединив сомножители в группы наиболее удобным для умножения способом, снова выполнить умножение. Какие законы умножения вы применяли?
420. (Устно.) Кузнечик длиной 1/20 м делает скачок в 75 раз больше своей длины. Как велик скачок кузнечика? 421. 1) Высота Ключевской сопки (ил Камчатке) 4 900 м; высота Эльбруса (на Кавказе) приблизительно в 1 1/7 раза больше, чем высота Ключевской сопки, а высота пика Сталина (на Памире) в 1 19/56 раза больше, чем высота Эльбруса. Найти высоту Эльбруса и высоту пика Сталина. 2) Предельный возраст жизни березы и ольхи 150 лет, сосна живёт в 34/5 раза дольше берёзы, ель в 22/19 раза дольше, чем сосна, а мамонтовое дерево в 5 раз дольше ели. Определить предельный возраст жизни сосны, ели и мамонтового дерева. 422. 1) Длина прямоугольного поля 2 1/2 км, а ширина равна 2/5 его длины. Найти площадь поля (в гектарах). 2) Поле прямоугольной формы имеет длину 1 200 м, а ширина его равна 3/5 этой длины. 2/3 поля засеяно пшеницей. Сколько гектаров земли засеяно пшеницей? 423. 1) Комната формы прямоугольного параллелепипеда имеет длину 51/2 м, ширину 41/2 м и высоту 4 м. Найти объём комнаты. 2) Фабричный корпус формы прямоугольного параллелепипеда имеет длину 60 м. Ширина корпуса составляет 2/3 его длины, а высота корпуса 3/10 ширины. Определить объём этого корпуса.
|